FQ-ViT: Post-Training Quantization for Fully Quantized Vision Transformer
Abstract
most existing quantization methods have been developed mainly on Convolutional Neural Networks (CNNs), and suffer severe degradation when applied to fully quantized vision transformers.
In this work, we demonstrate that many of these difficulties arise because of serious inter-channel variation in LayerNorm inputs, and present, Power-of-Two Factor (PTF), a systematic method to reduce the performance degradation and inference complexity of fully quantized vision transformers.
In addition, observing an extreme non-uniform distribution in attention maps, we propose Log-Int-Softmax (LIS) to sustain that and simplify inference by using 4-bit quantization and the BitShift operator.
Introduction
Up or Down? Adaptive Rounding for Post-Training Quantization
https://arxiv.org/abs/2004.10568
we propose AdaRound, a better weight-rounding mechanism for post-training quantization that adapts to the data and the task loss.
AdaRound is fast, does not require fine-tuning of the network, and only uses a small amount of unlabelled data.
By approximating the task loss with a Taylor series expansion, the rounding task is posed as a quadratic unconstrained binary optimization problem.
We simplify this to a layer-wise local loss and propose to optimize this loss with a soft relaxation.
Rounding-to-nearest is the predominant approach for all neural network weight quantization work that came out thus far.
Task-loss-based rounding
To avoid the computational overhead of repeated forward passes through the data, we utilize the second order Taylor series approximation. Additionally, we ignore the interactions among weights belonging to different layers.
This, in turn, implies that we assume a block diagonal H(w) , where each non-zero block corresponds to one layer. We thus end up with the following per-layer optimization problem.
For a converged pretrained model, the contribution of the gradient term for optimization can be safely ignored. This results in
From Taylor expansion to local loss
AdaRound
We take this as objective:
where ||·||^2 _F denotes the Frobenius norm and W~ are the soft-quantized weights that we optimize over
V_i,j is the continuous variable that we optimize over and h (Vi, j) can be any differentiable function that takes values between 0 and 1, i.e., h (V_i, j) ∈ [0, 1].
The additional term f_reg (V) is a differentiable regularizer that is introduced to encourage the optimization variables h (Vi, j) to converge towards either 0 or 1, i.e., at convergence h (Vi,j) ∈ {0, 1}.
The rectified sigmoid is defined as
where σ(·) is the sigmoid function and, ζ and γ are stretch parameters, fixed to 1.1 and −0.1, respectively.
Then we would perform the quantization layer by layer.
Q-BERT: Hessian Based Ultra Low Precision Quantization of BERT
https://arxiv.org/pdf/1909.05840.pdf
In this work, we perform an extensive analysis of fine-tuned BERT models using second order Hessian information, and we use our results to propose a novel method for quantizing BERT models to ultra low precision. In particular, we propose a new group-wise quantization scheme, and we use a Hessian-based mix-precision method to compress the model further.
A Hessian AWare Quantization (HAWQ) is developed for mixed-bits assignments. The main idea is that the parameters in NN layers with higher Hessian spectrum (i.e., larger top eigenvalues) are more sensitive to quantization and require higher precision, as compared to layers with small Hessian spectrum (i.e., smaller top eigenvalues).
Group-wise Quantization

Revisit LayerNorm and Softmax
Firstly, we find a serious inter-channel variation of LayerNorm inputs, which some channel ranges even exceed 40× of the median. Traditional methods cannot handle such large fluctuations of activations, which will lead to large quantization error.
Secondly, we find that the values of the attention map have an extreme non-uniform distribution, with most values clustered in 0 ∼ 0.01, and a few high attention values close to 1.
Methodology
Preliminary
Assuming the quantization bit-width is b, the quantizer Q(X|b) can be formulated as a function that maps a floating-point number X ∈ R to the nearest quantization bin:
Quantization Styles
Uniform Quantization is well-supported on most hardware platforms. Its quantizer Q(X|b) can be defined as:
where s (scale) and zp (zero-point) are quantization parameters determined by the lower bound l and the upper bound u of X, which are usually minimum and maximum:
Log2 Quantization converts the quantization process from linear to exponential variation. Its quantizer Q(X|b) can be defined as:
Power-of-Two Factor for LayerNorm Quantization
During inference, LayerNorm [Ba et al., 2016] computes the statistics µX, σX in each forward step and normalizes input X.
The above process can be written as:
It is observed that the channel-wise ranges fluctuate more wildly in vision transformers than those in ResNets.
Based on such extreme inter-channel variation, layer-wise quantization, which applies the same quantization parameters to all channels, will lead to an intolerable quantization error.
A possible solution is using group-wise quantization or channel-wise quantization.
The core idea of Power-of-Two Factor(PTF) is to equip different channels with different factors, rather than different quantization parameters.
Given the quantization bit-width b, the input activation X ∈ RB×L×C , the layer-wise quantization parameters s, zp ∈ R1 , and the PTF α ∈ N^C , then the quantized activation X_Q can be formulated as:
with
Noticing c represents the channel index for X and α. The hyperparameter K could meet different scaling requirements.
To cover the different inter-channel variation across all models, we set K = 3 as default.
BitShift
Meanwhile, thanks to the nature of powers of two, PTF α can be efficiently combined with layer-wise quantization by BitShift operator, avoiding floating-point calculations of group-wise or channel-wise quantization. The whole process can be processed with two phases:
Phase 1:
Phase 2:
Log-Int-Softmax for Softmax Quantization
Log2 Quantization for Attention Map
We quantize attention maps to lower bit-width.
Inspired by the idea of sparse attention in DynamicViT [Rao et al., 2021], we probe into the distribution of attention maps.
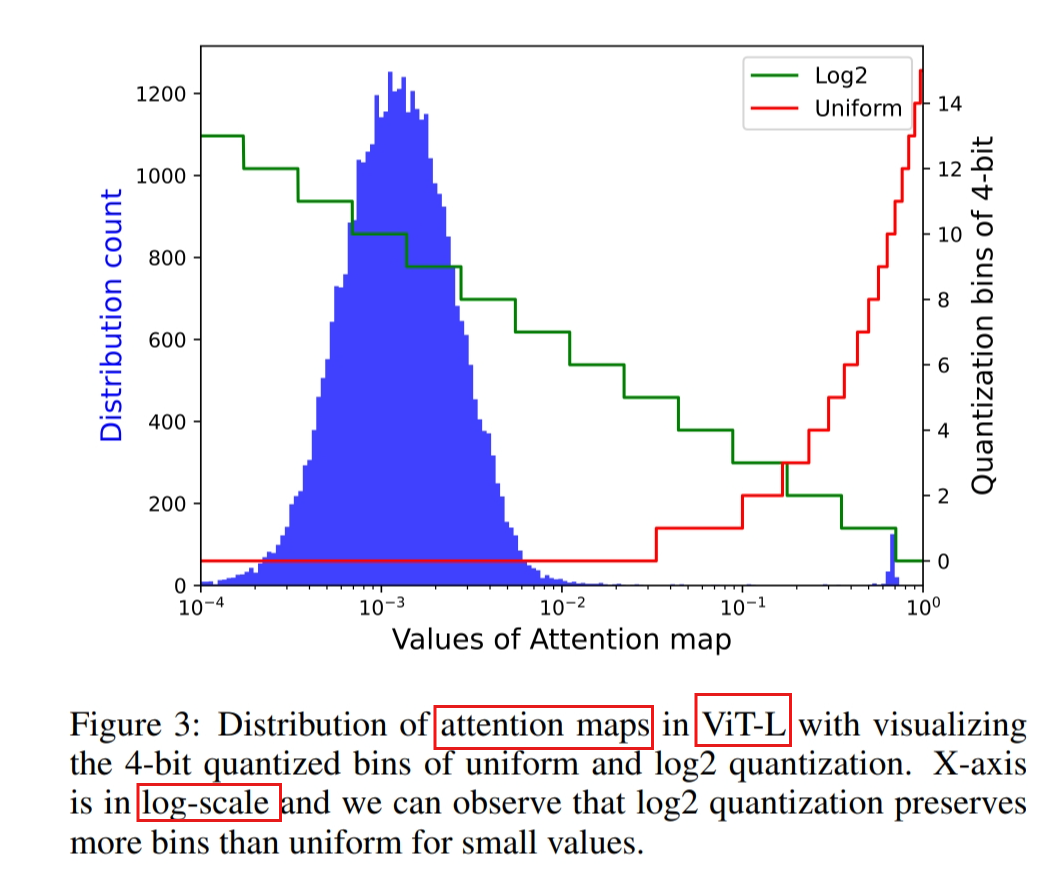
Moreover, following the purpose of ranking-aware loss [Liu et al., 2021b], log2 quantization can retain much order consistency between full precision and quantized attention maps.
Firstly, the fixed output range (0, 1) of Softmax makes the log2 function calibration-free:
This ensures that the quantization of attention maps will not be affected by the fluctuation of calibration data.
Secondly, it also introduces the merits of converting the MatMul to BitShift between the quantized attention map (AttnQ) and values (VQ) as:
with N = 2 ^ b - 1.
Noticing that directly right shift VQ with the results of AttnQ may lead to severe truncation error,
Integer-only Inference
However, data moving between CPU and GPU/NPU, doing dequantization and requantization, will induce great difficulties in hardware design, which is not a negligible consumption.
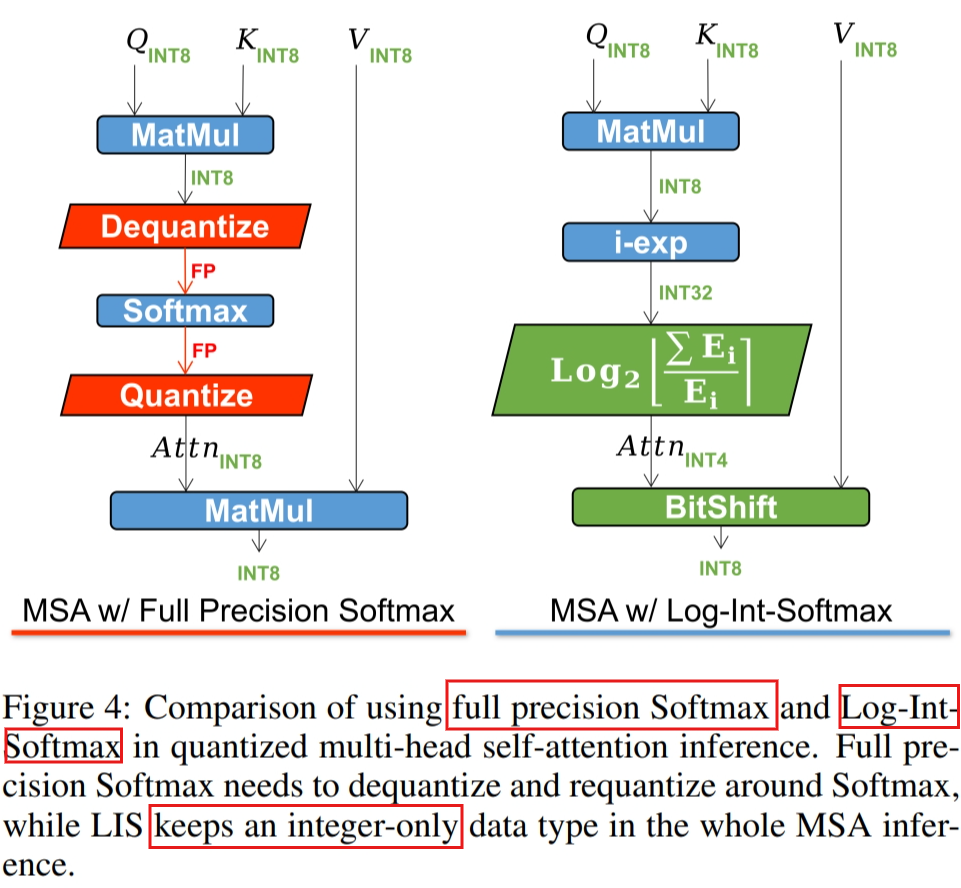
Combining log2 quantization with i-exp [Kim et al., 2021], which is a polynomial approximation of exponential function, we propose Log-Int-Softmax, an integer-only, faster, low consuming Softmax:
with N = 2 ^ b − 1